畳庵〜tatamiya practice〜

機械学習・統計モデリング練習帳。読書・source code読みの記録や，実装など。

statsmodelsによる状態空間モデリングを、KFASから「翻訳」して学ぶ（R経由で学ぶPythonの状態空間時系列モデリング#2）

Python R 時系列分析 状態空間モデル statsmodels

はじめに

この記事では、Pythonで状態空間時系列モデリングを行う方法を、Rによる実行例の「翻訳」を通して解説します。 題材として季節変動のある時系列データを用います。

状態空間時系列モデルでは、季節性やトレンドといった時系列背後の構造を反映させて直感的にわかりやすいモデリングを行うことができます。

しかし、Pythonで状態空間時系列モデリングを行おうことは、簡単ではありません。 Pythonで統計モデリング全般を実行する場合、ライブラリの選択肢はほぼstatsmodels1一択となります。しかし、このライブラリはインターフェイスが複雑で使いづらいうえにドキュメントも読みにくいのが現状です。 また、書籍やWeb情報も数えるほどしか見つかりません。

一方で、Rであれば学習環境がPythonに比べて恵まれています。RにはKFAS2, dlm3といった状態空間時系列モデルに特化した定番ライブラリが存在します。また、解説書籍・Web情報もPythonと比べて多く出ています。

そこで今回は、Pythonによる状態空間時系列モデリングのハードルを下げるために、まずはRでモデリングを行い「お手本」を作ります。そしてRによる出力結果を再現しながらPythonでモデリングの学習を行います。 具体的には季節変動をもつデータについてRのKFASで予測と成分分解を行い、同一の結果をPythonでstatsmodelsを用いて再現する方法を解説します。 記事の構成は以下のようになっています：

  1. 状態空間モデルで季節変動のある時系列を表現する方法を解説する
  2. KFASを用いてRで予測・状態推定を行う
    • 長期予測
    • 季節成分とレベル成分の分離
  3. KFASによる出力結果をstatsmodelsで再現する

なお、この記事は状態空間時系列モデリングについて解説する全5本の記事の3本目となっています。

f:id:tatamiyatamiyatatatamiya:20210212134022p:plain:w500

状態空間モデルの概要や線型ガウスモデルのカルマンフィルタによる扱いについては、前回までの記事を参照してください。

  • はじめに
    • 忙しい人のために
  • 状態空間モデルによる季節変動のある時系列データの扱い方
    • 線型ガウス状態空間モデル（前回の復習）
    • ローカルレベルモデル
    • ローカルレベル+季節成分モデル
  • KFASによるモデル構築
    • 基本的なモデル構築方法
      • モデルの定義
      • ハイパーパラメータ推定
    • 予測・推定結果
      • 長期予測
      • 成分ごとの推定
  • statsmodelsによるモデル構築
    • 基本的なモデル構築方法
      • モデルの定義
      • ハイパーパラメータ推定 + 平滑化
    • 予測・推定結果
      • 長期予測
      • 成分ごとの推定
    • KFASと比べて取得しにくい量
      • 成分ごとの長期予測
      • 成分和の予測・推定
  • まとめ
  • 参考資料

忙しい人のために

  • レベル成分を\mu_t、季節成分を\gamma_tとし、以下のようなローカルレベル+季節成分モデルを考える：
{ \begin{aligned} y_t &= \mu_t + \gamma_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= \mu_t + \eta^{(\mu)}_t, \quad \eta^{(\mu)}_t \sim N(0, \sigma_{\mu}^2)\\ \gamma_{t+1} &= - \gamma_t - \gamma_{t-1} - \gamma_{t-2} + \eta^{(\gamma)}_t,\quad \eta^{(\gamma)}_t \sim N(0, \sigma_\gamma^2) \end{aligned} }
  • RのライブラリKFASを用いてモデル構築を行えば、以下の予測・推定結果をpredict関数を用いて取得できる：
    • 観測値の長期予測: P(y _ {T+i}|Y _ {1:T})
    • 成分別の推定・予測
      • レベル成分: P(\mu_t|Y _ {1:T})
      • 季節成分: P(\gamma_t|Y _ {1:T})
      • レベル成分+季節成分: P(\mu_t + \gamma_t|Y _ {1:T})
  • PythonのライブラリstatsmodelsのUnobservedComponentsクラスを用いれば、KFASと同様のモデリング結果を再現できる。
  • 使い勝手の面では、statsmodelsはKFASに劣る

  1. https://www.statsmodels.org/stable/index.html↩

  2. https://cran.r-project.org/web/packages/KFAS/KFAS.pdf↩

  3. https://cran.r-project.org/web/packages/dlm/dlm.pdf↩

続きを読む

R経由で学ぶPythonの状態空間時系列モデリング#1: 逐次推定法とカルマンフィルタ

時系列分析 状態空間モデル

はじめに

概要

この記事は、状態空間時系列モデリングを解説する全5本の記事の第2弾です。

前回の記事では、状態空間モデルの概要について紹介しました。

状態空間モデルでは、トレンドや季節性といった時系列の特徴をマルコフ過程に従う「状態」として仮定し、観測データをもとに状態の予測・推定を行います。

tatamiya-practice.hatenablog.com

今回は状態推定方法のうち逐次推定法と呼ばれるものの概要から入り、カルマンフィルタについて解説を行います。

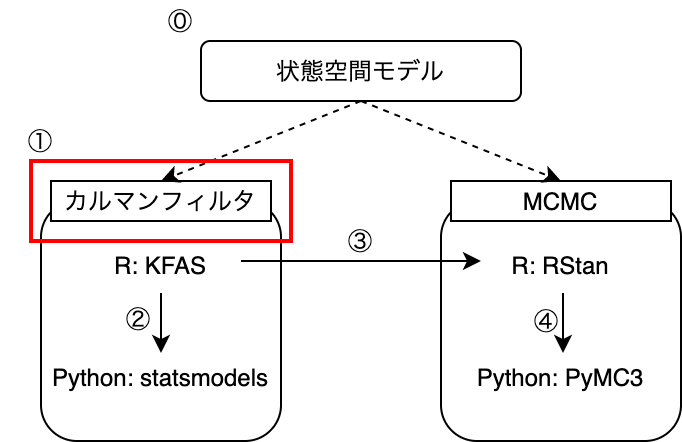
状態推定・予測の方法には、大きく分けて逐次推定法とMarkov Chain Monte Carlo法(MCMC)の2種類があります。

このうち前者の逐次推定法については、モデルが線型かつシステムノイズ・観測ノイズがガウス分布に従う場合、カルマンフィルタといって近似やサンプリングに頼らず厳密に推定値・予測値の分布を求めることができます。

線型ガウスのモデルは状態空間時系列モデリングでも基本となり応用範囲も広いため、 カルマンフィルタはKFASやstatsmodelsといった多くのライブラリで実装されています。

そこで今回は逐次推定法とカルマンフィルタの仕組みを理解することで、次回以降ライブラリを用いてモデリングを行う際に、出力された値がどのような過程を経て算出されたか、処理の裏でどのような演算が行われているかイメージできるようになることを目指します。

f:id:tatamiyatamiyatatatamiya:20210110150254p:plain:w500

当初の予定では今回の記事でKFASを用いたRによる実行方法も解説する予定でしたが、理論面で解説する内容が膨らんだため、次回に回すことにしました。

なお、カルマンフィルタの漸化式などの詳細な導出は今回は行いません。

  • はじめに
    • 概要
    • 忙しい人のために
  • 問題設定
  • 逐次推定法の考え方
    • 一期先予測とフィルタリング
    • 平滑化
    • 長期予測
  • カルマンフィルタ
    • 線型ガウスの状態空間モデル
    • 一期先予測における平均ベクトルと共分散行列の漸化式
    • 平均ベクトルと共分散行列の漸化式（結果のみ）
      • 一期先予測＋フィルタリング
      • 平滑化
      • 長期予測
  • まとめ
  • 参考文献

忙しい人のために

  • 状態空間モデリングで重要になる推定量は、観測値Y _ {1:T}=\lbrace y _ t\rbrace _ {t=1}^{\rm T}をもとにした状態\alpha _ tの事後分布P(\alpha _ t|Y _ {1:T})と（長期）予測分布P(\alpha _ {T+i}|Y _ {1:T})である。
  • 逐次推定手法では、以下のステップで事後分布P(\alpha _ t|Y _ {1:T})と予測分布P(\alpha _ {T+i}|Y _ {1:T})を推定する
    • 一期先予測分布P(\alpha _ t|Y _ {1:t-1})とフィルタリング分布P(\alpha _ t|Y _ {1:t})を交互に求めながら、時間順方向に１ステップずつ前進する。
    • P(\alpha _ T|Y _ {1:T})まで求めたら時間逆方向に１ステップずつ遡り事後分布P(\alpha _ t|Y _ {1:T})を推定する（平滑化）
    • P(\alpha _ {T}|Y _ {1:T})から時間順方向に１ステップずつ長期予測P(\alpha _ {T+i}|Y _ {1:T})を行う

f:id:tatamiyatamiyatatatamiya:20210110150615p:plain

  • 線型ガウスのモデルの場合、サンプリングや近似に頼らず推定値・予測値の分布を求められる（カルマンフィルタ）
    • 共分散行列と平均値の漸化式を解いていく
続きを読む

R経由で学ぶPythonの状態空間時系列モデリング#0: 状態空間モデルの概要

時系列分析 状態空間モデル Python R ベイズ推定

はじめに

内容

  • 状態空間時系列モデルの概要
    • 状態空間モデルとは何か？
    • 典型的なモデルの紹介
  • 今後の記事の執筆方針
    • 本記事あわせて全5本で構想中

背景

  • 状態空間モデルは時系列分析でよく用いられる手法の一つ
  • Pythonユーザーにとっては情報が少なくややとっつきにくい
    • Rと比べて書籍が圧倒的に少ない
    • ライブラリもRほど充実していない
    • ネットの情報も少ない
  • 理論の紹介 → Rでの実装例 → Pythonへの翻訳のステップを踏むことで、Pythonでも理論を理解したうえで状態空間モデリングを行えるようにしたい。
  • そのためにまずは、そもそも状態空間モデルとはどのようなもので、どのような実装方法があるかの全体像を把握する。

TL;DR

  • 状態空間モデルでは、現象の背後に状態を仮定し、観測値から状態の推定・予測を行う。
  • 状態空間時系列モデルは、トレンドや季節性といった構造を取り入れられ、解釈もしやすい。
  • 代表的なモデルとして、以下の3種類を挙げる
    • ローカルレベルモデル
    • 2次のトレンドモデル
    • ローカルレベル+季節成分モデル
  • 今後執筆予定の記事では、上記の3モデルの計算例とともに、下記の軸に沿って解説を行う
    • 状態推定手法: カルマンフィルタとベイズの比較
    • 実装方法: RからPythonへの翻訳
  • はじめに
    • 内容
    • 背景
    • TL;DR
  • 状態空間モデリングとは？
    • 概要
    • 線型ガウス状態空間モデルの例
      • 1. ローカルレベルモデル
      • 2. 2次のトレンドモデル
      • 3. ローカルレベル+季節成分モデル
  • まとめと今後の執筆方針
    • 現段階での記事構想
    • 今回の一連の記事では扱わないこと
      • ARIMAモデル
      • PyStan
      • 細かい式の導出
      • 非線形や非ガウスの状態空間モデル
  • 参考資料
    • データの出典
    • 書籍
続きを読む

NumPyでフーリエ変換を計算するためのメモ〜sin, cosで展開したときの係数をどう読み取るか〜

時系列分析 信号処理 Python

はじめに

内容

  • numpy.fft.fft/rfftの返り値は何を表しているか？
  • numpy.fft.fft/rfftの出力値から、\sin, \cosでFourier変換した表現に書き直すにはどうすればいいか？
    • その際、データ数の偶奇で出てくる項・和の範囲が異なるのは何故か？

背景

  • Fourier変換は時系列データの周期性を調べるときによく使われる
    • 時系列を三角関数の重ね合わせとして表現する
  • PythonでFourier変換を計算してみようとすると、引っかかる点が多い
    • numpy.fftは指数関数表現をもとにしている
    • 指数関数表現だと複素数が出てきてイメージがしにくい
    • 指数関数表現と三角関数表現の対応がわかりにくい
      • 周波数成分ごとに和をとる際、両者で和の範囲が異なる
      • 三角関数表現では、入力データ数の偶奇で処理の仕方が異なる
  • 三角関数表現をイメージをしながらnumpy.fftを触れるように、対応関係を整理したい。

TL;DR

  • 長さTの時系列データ\left \lbrace y_t \right \rbrace_{t=0}^{T-1}をnumpy.fft.fftでFourier変換した際の返り値の中身は、以下に示す指数関数表現の係数である：
{ \begin{aligned} c_k &= \sum_{t=0}^{T-1} y_t \exp \left(- i \frac{2\pi k}{T} t \right) \\ \end{aligned} }
  • 三角関数を用いて展開した際の係数との対応は、以下のようになっている：
{ \begin{aligned} y_t &= c + \sum_{k=1}^{M} a_k \cos\left( \frac{2\pi k}{T} t\right) + \sum_{k=1}^{M} b_k \sin\left( \frac{2\pi k}{T} t\right) \\ \end{aligned} }
{ \begin{aligned} c = \frac{1}{T} (c_0 + c_{T/2}) \end{aligned} }
{ \begin{aligned} a_k = \frac{2}{T} \,{\rm Re}\,c_k, \quad b_k = - \frac{2}{T} \,{\rm Im}\,c_k\\ \end{aligned} }

ただし、

{ \begin{aligned} M= \begin{cases} (T-1)/2 \quad & T: {\rm 奇数}\\ T/2 -1 \quad & T: {\rm 偶数}\\ \end{cases} \end{aligned} }
{ \begin{aligned} c_{T/2}= \begin{cases} 0 \quad & T: {\rm 奇数}\\ \sum_{t=0}^{T-1}(-1)^ty_t \quad & T: {\rm 偶数}\\ \end{cases} \end{aligned} }
  • 三角関数表現にてデータ長Tの偶奇で計算方法が異なるのは、和\sum _ {k=0}^{T-1}をとる際に複素共役の関係c _ {T-k} = c_k^*を利用してT/2で折り返しc_kとc_{T-k}でペアを作るためである。
  • 入力データが実数であれば、numpy.fft.rfftを使って計算するのが便利である
  • はじめに
    • 内容
    • 背景
    • TL;DR
  • 序章：Fourier変換とはどのようなものか？
  • NumPyでFourier変換を行う方法
    • numpy.fft.fftの出力と指数関数を使った表現
    • 指数関数表現と三角関数表現の対応
  • numpy.fftを使って三角関数表現のFourier変換を行う
  • おわりに
  • 補足
    • 係数のかけかたのパターン
    • Eulerの公式の簡易な導出
  • 参考文献
続きを読む

Leap-frog法はなぜ誤差が蓄積しないのか？を視覚的に理解する〜Hamiltonian Monte Carlo法の補足の補足〜

ベイズ推定 MCMC

久々の更新、お久しぶりです。

最近このようなベイズ統計モデリングの本を共著で書きました：

PyMC3、Pyroで学ぶ統計モデリング発展

PyMC3、Pyroで学ぶ統計モデリング発展

自分の担当箇所は第二章のHamiltonian Monte Carlo法（以下HMC）の節と、AppendixのHMCの詳細です。

HMCは任意の確率分布からサンプリングを行う際に用いられる手法で、 StanやPyMCといった確率的プログラミングの裏の処理にも使われています。

この手法は物理学の考え方をベースとしておりとっつきにくいうえに、 PRMLなどの書籍でも簡単にしか触れられておらず読んでいてピンとこなかったので、自分なりに間を埋めて解説してみました。

kindle unlimitedなら無料で読めますので、もしご興味があれば手にっていただけると嬉しい限りです。

さて、この記事では、HMCで使われるLeap-frog法について、上掲書の補足を行います。

HMC法では、求めたい分布に従うような運動を表現するための力学モデルを作り、 運動方程式を差分法で解くことによってサンプル候補を作り出しています。

そして、運動方程式を数値的に解く際には、leap-frog法という特殊な差分法を用いています。

このleap-frog法は、大体どの書籍でもいきなり出てくるので、面食らったか狐に摘まれたような気分になった方も多数いるかと思います。

また、微分方程式の数値計算手法を勉強したことのある人からすると、なぜEuler法やRunge-Kutta法といった一般的な手法を使わないのだろう？ という疑問が湧いたかと思います。

上掲書の中でも解説しましたが、leap-frog法を用いる理由は、

  • 数値計算誤差が蓄積していかないから
  • 時間反転対象性がMetropolis法を適用するうえで不可欠だから

ということが挙げられます。

このうち前者の数値計算誤差について、ハミルトニアンとは別に「影のハミルトニアン」という別の保存量が存在するから真の軌道に限りなく近い数値軌道が得られる、との補足を入れました。

詳細に突っ込みすぎるため本の中ではそれ以上の言及は控えましたが、 これだけ読んでもあまりにも抽象的でよくわからないぞ、という感想が大半だろうと思いますので、 この場にて「補足の補足」をさせていただきます。

  • この記事の内容
    • 目的
    • 伝えたいこと
    • 話さないこと
  • Leap-frog法
    • 復習
    • 単振動におけるleap-frog法の数値軌道
  • Euler法、Runge-Kutta法との比較
    • Euler法
    • Runge-Kutta法
  • まとめ
    • 参考文献
  • 補足：単振動の影のハミルトニアンの導出
    • 差分式の行列表記
    • 固有値分解による保存量の表現
    • 保存量の座標逆変換

この記事の内容

目的

Leap-frog法ではなぜ誤差が蓄積していないかを、一次元単振動を例に、他の一般的なアルゴリズムとの比較を通して視覚的に理解する

伝えたいこと

  • Leap-frog法で誤差が蓄積しない理由は、真の軌道に近い閉じた軌道を描くからである
    • 刻み幅を小さくすればするだけ厳密な軌道に連続的に近づく
    • 一方で、他の手法ではどんなに刻み幅を小さくしようが軌道が発散or収束してしまう

話さないこと

  • 物理の基本（運動方程式など）
    • ハミルトン方程式については冒頭で紹介した本にも簡単な導入があります。
  • HMCのアルゴリズムの解説
    • 気になる方は、是非PRMLや、冒頭の本を手にお取りください。
  • 一般に影のハミルトニアンが存在することの証明
    • 単振動における影のハミルトニアンの求め方については、最後に補足という形で解説します。
続きを読む

User, Itemメタ情報を埋め込んだレコメンドアルゴリズムLightFM詳解

レコメンド 協調フィルタリング Matrix Factorization SVD Python Factorization Machines

本記事では，LightFM(Kula, 2015)というレコメンドアルゴリズムについて，論文とGitHubの実装を読んで筆者が得た理解に基づき解説します。

arxiv.org

github.com

前回，前々回と，行列分解ベースのレコメンド手法に関する話題で記事を書きました：

tatamiya-practice.hatenablog.com

tatamiya-practice.hatenablog.com

こちらの手法ではUserのItemに対する評価履歴を行列で表し因子分解しました。

それに対しLightFMではその枠組みを拡張し，各分解要素をUser / Itemメタ情報の線型式でモデリングします。

  • 導入：Matrix Factorizationからの流れ
    • Matrix Factorizationの復習
    • Matrix Factorizationの限界とコールドスタート問題
  • LightFM
  • 関連手法
    • Matrix Factorizationとの対応
    • Factorization Machinesとの関係
  • おわりに
    • MF × LightFM = FM
    • 今回触れられなかったこと
  • 補足：SGDにおけるパラメータ更新式の導出
続きを読む

画像に直接レコメンドアルゴリズムを適用してみる〜通常の特異値分解とレコメンドのMatrix Factorizationで行列分解比較〜

レコメンド 協調フィルタリング SVD Matrix Factorization 特異値分解

昨日の記事で，レコメンドアルゴリズムを視覚的に理解するということで，FunkのMatrix Factorizationによる出力値をヒートマップにして表し，入力したUser-Item行列との比較を行いました。

tatamiya-practice.hatenablog.com

この中で，

  • 出力レコメンド評価値は「バイアス項＋行列分解項」から成る
  • 行列分解項は入力行列を再現する方向に補正を行う
  • 因子数 dが大きくなるほど入力画像の再現度が高くなる

という解釈を行いました。

今回はこれを確かめるために，画像をUser-Item行列に見立ててFunkのレコメンドアルゴリズムを適用して， dが入力画像の列/行数に近づくにつれ出力が入力に近づいていくかを見ました。

例によって，実行コードは下記にアップしてあります。

numpyとscikit-learnで画像の特異値分解を試した。 · GitHub

Applying Recommendation Algorithms Directly to an Image Itself · GitHub

方法

入力画像

以下の謎のカボチャ画像を使います。

f:id:tatamiyatamiyatatatamiya:20200308135641p:plain

こちらは行数766列数796の行列で，ピクセル値が[0, 1]の範囲で入っています。

これを行: User, 列: ItemのUser-Item行列と見立て，行列分解を行います。

適用アルゴリズム

上記の２手法で画像を行列分解したのち，因子数 dで再構成します。

dを変えながら，両手法の再構成後の画像の違いを見ていきます。

結果

因子数 d 通常の特異値分解 Funkのレコメンドアルゴリズム
1 f:id:tatamiyatamiyatatatamiya:20200308141303p:plain f:id:tatamiyatamiyatatatamiya:20200308140922p:plain
5 f:id:tatamiyatamiyatatatamiya:20200308141313p:plain f:id:tatamiyatamiyatatatamiya:20200308141009p:plain
766 f:id:tatamiyatamiyatatatamiya:20200308141328p:plain f:id:tatamiyatamiyatatatamiya:20200308141705p:plain

考察

両手法とも因子数 dを上げるほど入力画像に近づいていきます。

しかし，通常の特異値分解では dが入力行数である766に達した段階で元の画像が完璧に再現されるのに対して，Funkのレコメンドアルゴリズムではぼやけたままです。 *1

この違いは，Funkの方法ではバイアス項が加わっているためと考えられます。

Funkのレコメンドアルゴリズムの結果をよくみると， dが大きくなっても縦横の帯状の模様が残り続けるのが見て取れます。

Funkの方法で導入されたバイアス項は，User-Item行列で見た縦横の平均的な値を反映しているので，その影響として理解できそうです。

おわりに

やはり因子数 dを大きくすると，入力を再現する方向に出力が変化していくようです。

ただし，入力画像と出力画像の誤差をRMSEやMAEで評価すると，画像では dを大きくするについれ一様に誤差が小さくなっていくのに対して，User-Item行列ではある最適値以上では逆に誤差が大きくなっていくという違いがありました。（冒頭に貼ったURLを参照）

これについてははっきりと理由はわからないですが，入力データの滑らかさなどといった性質の違いに依存しそうです。

*1:特異値分解では原理的に dの最大値は入力行列のRankと一致し，この時厳密に入力行列が再現されます。一方でFunkのレコメンドアルゴリズムでは最適化手法により最も入力行列との誤差が小さくなる分解方法を探すので， dをいくらでも大きくできます。（ただ，パラメータ数が増えるので計算時間はかなり長くなりますが，，，）