はじめに

内容

状態空間時系列モデルの概要
- 状態空間モデルとは何か？
- 典型的なモデルの紹介
今後の記事の執筆方針
- 本記事あわせて全5本で構想中

背景

状態空間モデルは時系列分析でよく用いられる手法の一つ
Pythonユーザーにとっては情報が少なくややとっつきにくい
- Rと比べて書籍が圧倒的に少ない
- ライブラリもRほど充実していない
- ネットの情報も少ない
理論の紹介 → Rでの実装例 → Pythonへの翻訳のステップを踏むことで、Pythonでも理論を理解したうえで状態空間モデリングを行えるようにしたい。
そのためにまずは、そもそも状態空間モデルとはどのようなもので、どのような実装方法があるかの全体像を把握する。

TL;DR

状態空間モデルでは、現象の背後に状態を仮定し、観測値から状態の推定・予測を行う。
状態空間時系列モデルは、トレンドや季節性といった構造を取り入れられ、解釈もしやすい。
代表的なモデルとして、以下の3種類を挙げる
- ローカルレベルモデル
- 2次のトレンドモデル
- ローカルレベル+季節成分モデル
今後執筆予定の記事では、上記の3モデルの計算例とともに、下記の軸に沿って解説を行う
- 状態推定手法: カルマンフィルタとベイズの比較
- 実装方法: RからPythonへの翻訳

はじめに
- 内容
- 背景
- TL;DR
状態空間モデリングとは？
- 概要
- 線型ガウス状態空間モデルの例
まとめと今後の執筆方針
- 現段階での記事構想
- 今回の一連の記事では扱わないこと
参考資料
- データの出典
- 書籍

状態空間モデリングとは？

概要

状態空間モデルでは、観測され系列データ $y_t$ の背後に状態 $\alpha_t$ を仮定し、何かしらのルールで変化する $\alpha_t$ を観察した結果が $y_t$ である、と考えます。

このとき、観測 $\alpha_t \to y_t$ と状態変化 $\alpha_t \to \alpha_{t+1}$ は、マルコフ過程として描けるものと考えます：

${ \begin{aligned} y_t &\sim h(y|\alpha_t)\\ \alpha_{t+1} &\sim q(\alpha|\alpha_t) \end{aligned} }$

f:id:tatamiyatamiyatatatamiya:20201229201303p:plain — 状態空間モデルの概念図

このようにある構造をもったデータ生成過程を仮定したうえで、観測データをもとに状態 $\alpha$ の推定・未来の予測を行うのが状態空間時系列モデリングです。

具体的には、以下のような量を計算します：

全観測値に基づく状態の推定値（平滑化状態）:
- $\hat{\alpha}_t = E\lbrack \alpha_t|Y_T \rbrack \quad (0\le t \le T)$
未来の観測値や状態の予測値
- 観測予測値: $\hat{y}_t = E\lbrack y _ {T+i}|Y_T\rbrack$
- 状態予測値: $\hat{\alpha}_{T+i} = E\lbrack \alpha _ {T+i}|Y_T\rbrack$

$E\lbrack \cdot|X \rbrack$ は $X$ が与えられたもとでの条件付き期待値です。

また、状態推定の方法はカルマンフィルタとMCMCの2種類が代表的です。

線型ガウス状態空間モデルの例

状態空間モデルの中でも比較的計算が容易でよく用いられるのが、以下の形で書ける線型ガウス状態空間モデルと呼ばれる種類のものです：

${ \begin{aligned} y_t &\sim N(Z\alpha_t, H)\\ \alpha_{t+1} &\sim N(T\alpha_t, RQR^T). \end{aligned} }$

$N(\mu, \Sigma)$ は期待値が $\mu$ , 共分散行列が $\Sigma$ の正規分布を表します。観測値 $y_t$ と状態 $\alpha_t$ はともにベクトルで表現しており、 $Z, H, T, R$ はいずれも行列です。

同じ内容を、表現を変えて書くと以下のようになります：

${ \begin{aligned} y_t &= Z\alpha_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, H)\\ \alpha_{t+1} &= T\alpha_t + R\eta_t, \quad \eta_t \sim N(0, Q) \end{aligned}\tag{1}\label{eq:dlm} }$

以下に3種類の線型ガウス状態空間モデルの代表的な例を、データへの適用例とともに紹介します。

なお、以下グラフでは、太い黒線は観測値 $y_t$ を、細い灰色線は状態推定値・予測値 $\hat{\alpha}_t$ を表しています。推定値の周りの帯は、状態推定値の分散 $V_t={\rm Var}\lbrack \alpha_t|Y_T \rbrack$ をもとに算出した25~75%, 10~90%の区間です。

1. ローカルレベルモデル

ローカルレベルモデルは、状態空間モデルの中でも最もシンプルなモデルです。

${ \begin{aligned} y_t &= \alpha_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \alpha_{t+1} &= \alpha_t + \eta_t, \quad \eta_t \sim N(0,\sigma_\eta^2) \end{aligned} }$

ブラウン運動する状態 $\alpha_t$ に、観測ノイズ $\varepsilon_t$ が乗る、と解釈ができます。

サンプルとして、以下のような架空の売り上げデータ（馬場2019）に適用しました：

f:id:tatamiyatamiyatatatamiya:20210212211017p:plain:w400 — ローカルレベルモデルによる架空の売り上げデータの状態推定・予測結果（太黒線： $y_t$ 、細灰線: $\hat{\alpha}_t$ 、データの出典：馬場2019）

ローカルレベルモデルによる架空の売り上げデータの状態推定・予測結果（太黒線： $y_t$ 、細灰線: $\hat{\alpha}_t$ 、データの出典：馬場2019）

2. 2次のトレンドモデル

前述のローカルレベルモデルで状態の式を

${ \begin{aligned} \Delta \alpha_{t+1} \equiv \alpha_{t+1} - \alpha_t \sim N(0, \sigma_\eta^2) \end{aligned} }$

のように書き直すと、変化の期待値が常に0、つまり平均的なトレンドのない系列、として解釈できます。

これに対して、時系列が明確なトレンドを持つと仮定する場合は、以下のようなモデルを考えます：

${ \begin{aligned} y_t &= \mu_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= 2 \mu_t - \mu_{t-1} + \eta_t, \quad \eta_t \sim N(0, \sigma_\mu^2) \end{aligned} }$

線型ガウスモデルの一般式(\ref{eq:dlm})とは、 $\alpha _ t \equiv (\mu _ t, \mu _ {t-1}) ^ T$ とおくと対応します。

今度は

${ \begin{aligned} \Delta \mu_{t+1} &= \Delta \mu_t + \eta_t, \quad \eta_t \sim N(0, \sigma_\mu^2) \end{aligned} }$

と書き換えられますので、トレンドがブラウン運動にしたがって少しずつ変化している、と解釈することができます。

先ほどと同じデータについて、このモデルにしたがって状態推定・予測を行うと次のようになります：

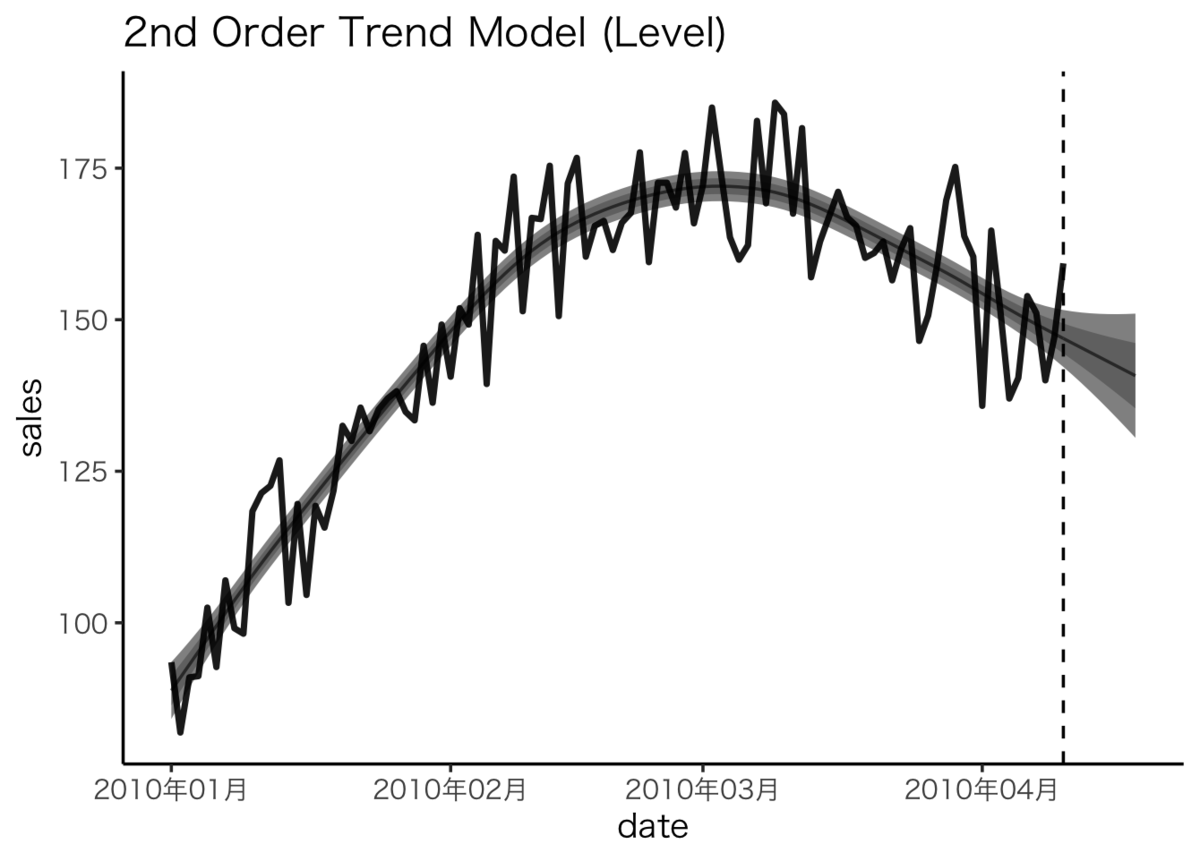
f:id:tatamiyatamiyatatatamiya:20210212211108p:plain:w400 — 2次のトレンドモデルによる架空の売り上げデータの状態推定・予測結果（太黒線： $y_t$ 、細灰線: $\hat{\mu}_t$ 、データの出典：馬場2019）

2次のトレンドモデルによる架空の売り上げデータの状態推定・予測結果（太黒線： $y_t$ 、細灰線: $\hat{\mu}_t$ 、データの出典：馬場2019）

ローカルレベルモデルと比べて滑らかな状態推定値 $\hat{\mu}_t$ が得られ、また予測値も直前までの傾きを外挿するように伸びています。

3. ローカルレベル+季節成分モデル

実世界のデータはトレンドに加えて、日・週・月・年といった何かしらの周期性を持っていることがよくあります。

そのような場合は、時系列 $y_t$ を以下のようにトレンド成分 $\mu_t$ ・季節成分 $\gamma_t$ ・ノイズ $\varepsilon_t$ の和に分解して表現します：

${ \begin{aligned} y_t = \mu_t + \gamma_t + \varepsilon_t \end{aligned} }$

季節成分 $\gamma_t$ は以下のように1周期分の和が平均的に0になるダミー変数として扱います¹：

${ \begin{aligned} \sum_{i=1}^{s}\gamma_{t+i} \sim N(0, \sigma_\gamma^2) \end{aligned} }$

上記では周期を $s$ としています。

以下に示すのは、ローカルレベルモデルに4半期周期成分を加えたモデルです：

${ \begin{aligned} y_t &= \mu_t + \gamma_t + \varepsilon_t, \quad \varepsilon_t \sim N(0, \sigma_\varepsilon^2)\\ \mu_{t+1} &= \mu_t + \eta^{(\mu)}_t, \quad \eta^{(\mu)}_t \sim N(0, \sigma_{\mu}^2)\\ \gamma_{t+1} &= - \gamma_{t} - \gamma_{t-1}- \gamma_{t-2} + \eta^{(\gamma)}_t,\quad \eta^{(\gamma)}_t \sim N(0, \sigma_\gamma^2) \end{aligned} }$